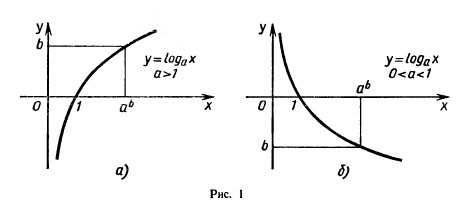
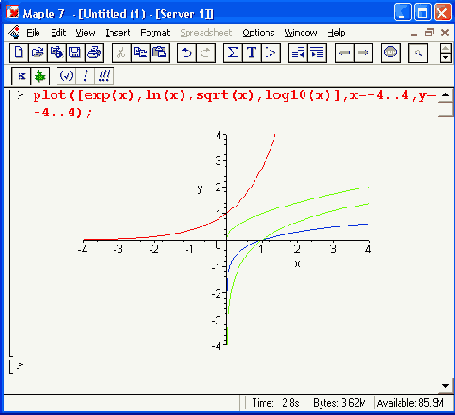
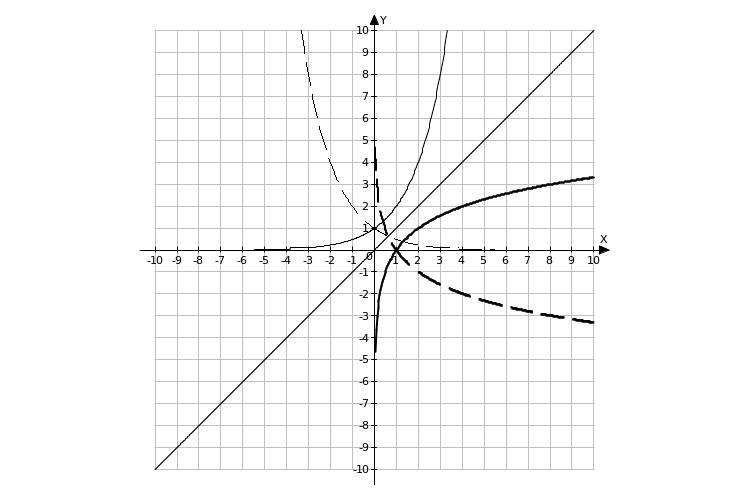
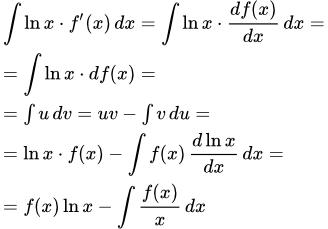Примеры логарифмирования натуральными логарифмами степенных функций
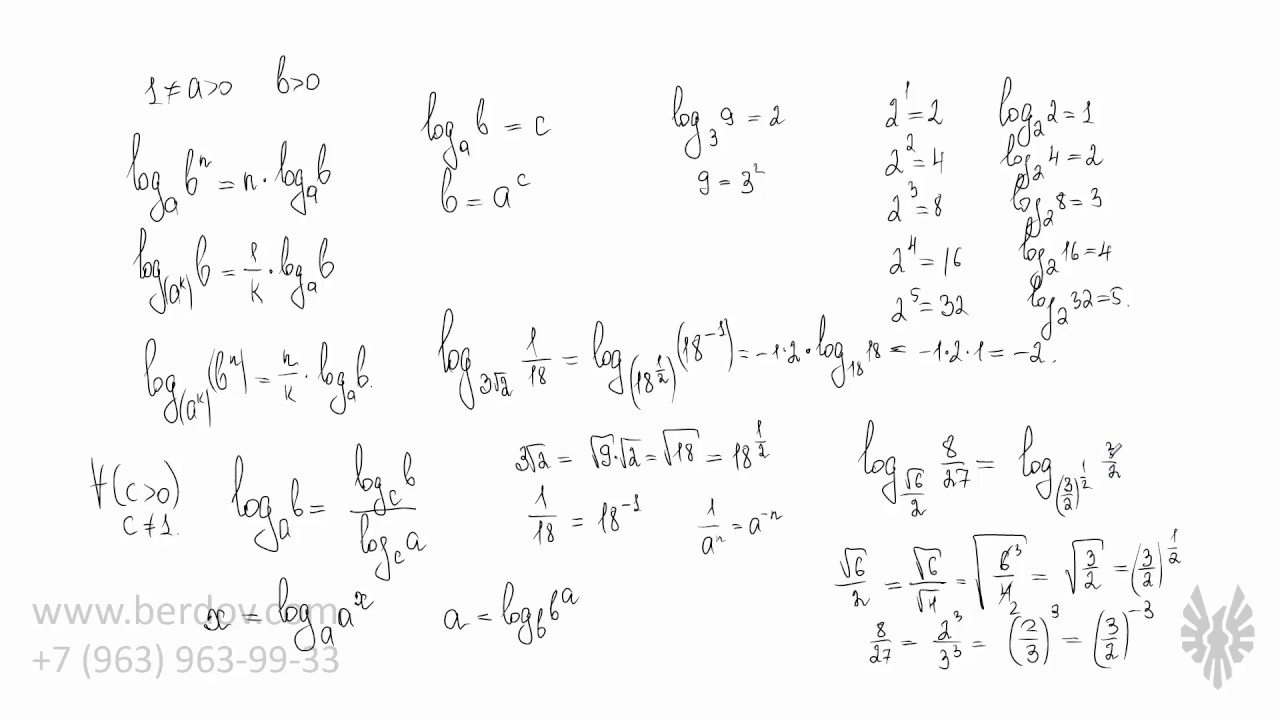
Решение логарифмических уравнений на ЕГЭ
Логарифмы обладают уникальными свойствами, которые определили их широкое использование для существенного упрощения трудоёмких вычислений [ 4 ]. При переходе «в мир логарифмов» умножение заменяется на значительно более простое сложение, деление — на вычитание, а возведение в степень и извлечение корня преобразуются соответственно в умножение и деление на показатель степени. Лаплас говорил, что изобретение логарифмов, «сократив труд астронома, удвоило его жизнь» [ 5 ].
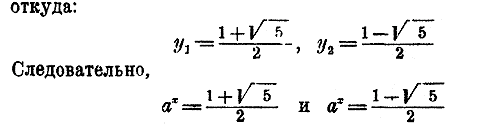




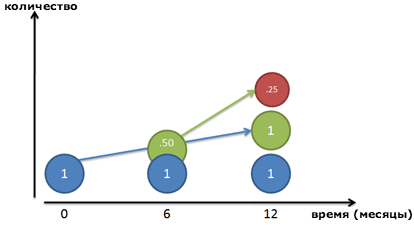

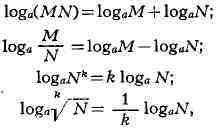
Вы знаете, какая тема в математике объединяет рога горных козлов, многие галактики и возможность получить 4 первичных балла на ЕГЭ по профильной математике? Это логарифм и его свойства! Но обо всем по порядку. Логарифмы — это математические функции, которые являются обратными к операциям возведения в степень.


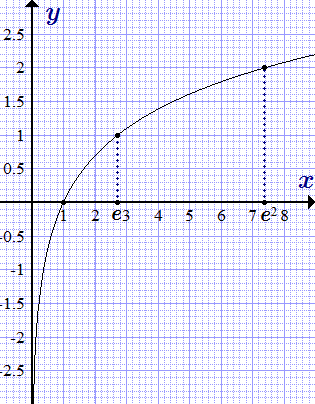


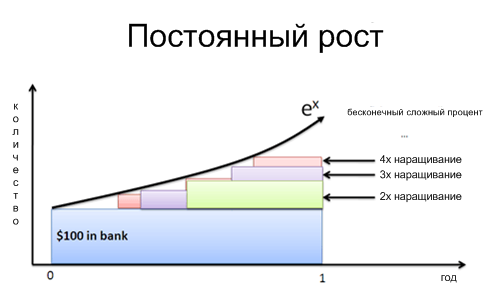

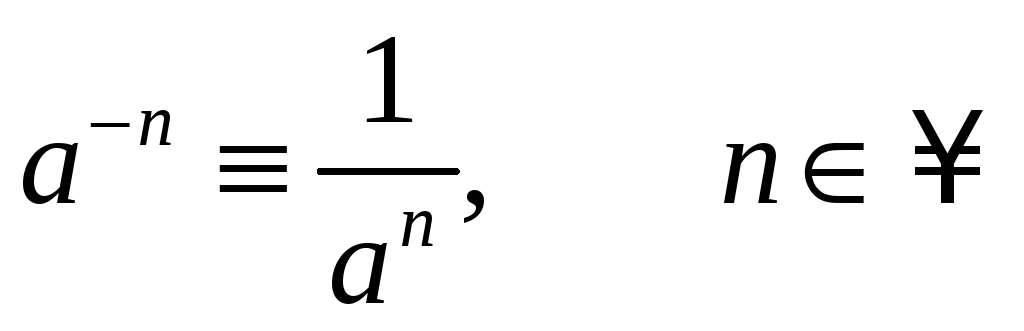
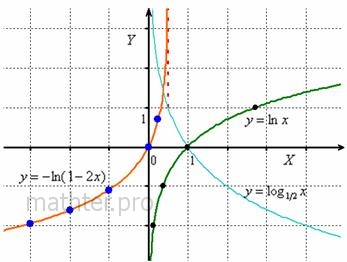

| 369 | Как и экспонента, логарифмическая функция относится к категории трансцендентных функций. Натуральные логарифмы полезны для решения алгебраических уравнений , в которых неизвестная присутствует в качестве показателя степени, они незаменимы в математическом анализе. | |
| 198 | Сегодня в этой статье мы с тобой обсудим, как решать простые и сложные логарифмические уравнения. | |
| 348 | Логарифмы Логарифмирование активно используются в решении задач , так как значительно упрощают обычные алгебраические операции. Использование логарифмов позволяет заменить умножение на значительно более простое сложение, деление — на вычитание, а возведение в степень и извлечение корня заменяются соответственно на умножение и деление на показатель степени числа. |
Из определения следует, что записи и равносильны. Основное логарифмическое тождество:. Логарифм произведения равен сумме логарифмов. Логарифм частного равен разности логарифмов.